|
Calculer avec les nombres complexes
|
|
-Cet exercice nécessite la conaissance du théorème second degré (version TS)-
|
Soit le polynôme P défini sur 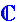 par P(z) = z³ - 8z² + 22z - 21. par P(z) = z³ - 8z² + 22z - 21.
1) Montrer que P(3) = 0.
|
|
|
On calcule en remplaçant z par 3,
P(3) = 3³ - 8*3² + 22*3 - 21
P(3) = 27 - 8*9 + 66 - 21
P(3) = 27 - 72 + 66 - 21
P(3) = -45 + 45
P(3) = 0
On a bien montré que P(3) = 0.
|
2) Montrer qu'il existe un polynôme Q de degré 2, à coefficients réels, tel que
pour tout nombre complexe z, P(z) = (z - 3)Q(z)
|
|
|
Si Q est de degré 2, Q est de la forme Q(z) = az² + bz + c
Q étant à coefficients réels, les coefficients a,b et c sont donc réels.
On cherche trois nombres réels a,b et c tels que : P(z) = (z - 3)( az² + bz + c )
On distribue :
P(z) = (z - 3)( az² + bz + c )
P(z) = z*( az² + bz + c ) - 3*( az² + bz + c )
P(z) = az³ + bz² + z*c - 3*az² - 3*bz - 3*c
P(z) = az³ + ( b - 3*a )z + ( c - 3*b ) - 3*c
Or P(z) = z³ - 8z² + 22z - 21, par identification des coefficients on obtient :
a = 1 ( coefficients de z³ )
b - 3*a = -8 ( coefficients de z² )
c - 3*b = 22 ( coefficients de z )
-3*c = -21 ( constantes )
On a donc a = 1, en remplaçant dans la deuxième équation on obtient :
b - 3*1 = - 8 soit b = - 5
En remplaçant b dans la troisième équation on obtient :
c -3*(-5) = 22 soit c = 7
La dernière équation permet de vérifier !
Donc pour tout complexe z, P(z) = (z - 3)(z² - 5z + 7)
|
3) En déduire les solutions dans 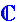 de l'équation P(z) = 0 de l'équation P(z) = 0
|
|
|
L'équation P(z) = 0 équivaut à (z - 3)(z² - 5z + 7) = 0
Un produit de facteur est nul si, et seulement si, un des facteurs est nul :
- Ou z² - 5z + 7 = 0
On calcule le discriminant :
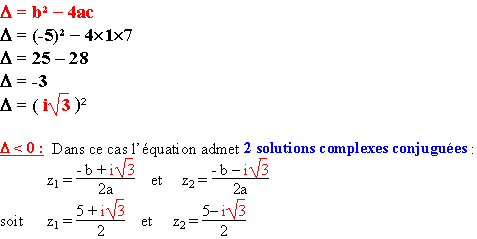
L'ensemble des solutions de l'équation P(z) = 0 est 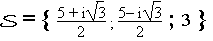
|
4) En déduire une factorisation dans 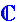 du polynôme P du polynôme P
|
|
|
D'après la question 2) P(z) = (z - 3)Q(z) avec Q(z) = z² - 5z + 7, polynôme de degré 2
possédant comme racines 
Donc d'après le théorème du cours sur le second degré, le polynôme Q
se factorise sous la forme 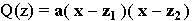
Donc 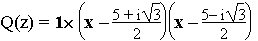
Par conséquent on factorise le polynôme P dans 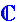 : :
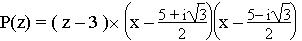
|